SPECTROSCOPY OF RADIO-WAVE EMISSIONS OF LOCALIZED PHOTONS: ACCESS TO QUANTUM-NON-LOCAL BIOINFORMATION PROCESSES
I.V.Prangishvili, P.P.Garyaev, G.G.Tertyshny, V.V.Maximenko, A.V.Mologin, E.A.Leonova, E.R.Muldashev.
Previously, we developed a laser facility, with the help of which we discovered the phenomenon of the transition of red coherent photons into broad-spectrum radio waves. We proposed a preliminary explanation for this phenomenon [21]. The present study proposed by the authors significantly supplements the provisions they have previously expressed and is a certain stage in the theoretical and experimental substantiation of a new type of spectroscopy of substances [ Priority for a patent dated 01/06/1999. No. 99/01/L (Federal Institute of Industrial Property. PCT Receiving Office Group. Starfield, Ltd.).]
With the code name – polarization laser-radio wave spectroscopy (PLR spectroscopy). Such spectroscopy is designed to study previously unknown, rotational-vibrational quantum-molecular characteristics of solid, liquid, gaseous substances, as well as plasma states. The proposed version of PLR spectroscopy uses a narrow optical range – red light, but in the future it is planned to use shorter wavelengths in the visible region.
For the purposes of PLR spectroscopy, a special He-Ne laser () was made with the generation of two optical modes orthogonally coupled in intensity, which can interact with each other in such a way that the sum of their intensities remains unchanged. When at least one mode interacts with a substance, the reflected or scattered radiation from which returns to the optical resonator, the intensity of these optical modes is redistributed according to the law of polarization change corresponding to the new state after the interaction of the beam with dynamic micropolarizers located in the cross section of the illuminated area of the substance under study. One of the laser modes, in a certain mode of generation, is capable, in the process of interaction with a substance, of causing the emission of broad-spectrum modulated radio waves by our installation, correlated with modulations in the optical modes of laser radiation. These modulations depend on the rotational vibrations of the microstructural components (for example, crystal domains) of the substances under study and their optical activity. Frequency interval induced radio waves, in accordance with the theoretical model (see below), lies in the range from 2 to 0. The maximum of such radio emission is located in the region of 1-3 MHz. After detection, the radio wave signal is fed to the ADC of a computer with a special processing program. At the output, the Fourier spectrum of radio emission is recorded, which characterizes the polarization-dynamic properties of the studied substances with which one of the laser beams interacts, as well as the spectral memory of the studied substances. The second beam then returns to the laser resonator to create resonant interaction with the atomic oscillators of the gas mixture. This laser is also capable of generating, in addition to the main (optical) frequency, radio waves of a wide range of wavelengths. We believe that the reason for this phenomenon is the inelastic scattering and localization of the light of the fundamental laser mode on the system of inhomogeneities of the laser resonator mirrors. The mechanism of localization (localization in an inelastic scattering channel) is described in detail. In particular, the position is put forward that elastically scattered localized light also exists in the resonator (see the theoretical part). Radio wave radiation generated by a laser is capable of “reading information”, for example, from DNA preparations (see the experimental part). The mechanism of “reading” resembles the mechanism of conventional stimulated emission. The ability to “open and close” the laser cavity allows you to localize or “record” in it your own “spectra” of various test objects. Radio wave radiation reads and retransmits such spectra. In this case, the effect of spectral memory was discovered: during a certain macroscopic time, the radio wave spectra of objects are reproduced, reflecting the beam back into the resonator and then removed from the exposure zone. Thus, DNA spectra were recorded and their high biological activity was revealed, probably associated with the wave type of transfer of genetic and metabolic information (see the experimental part).
Experimental part
PLR spectroscopy of minerals and biostructures. Spectral memory effect.
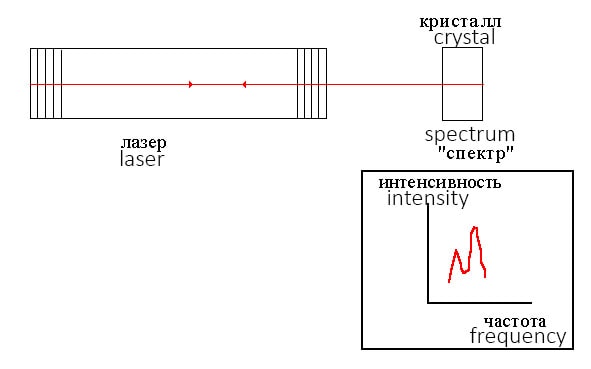
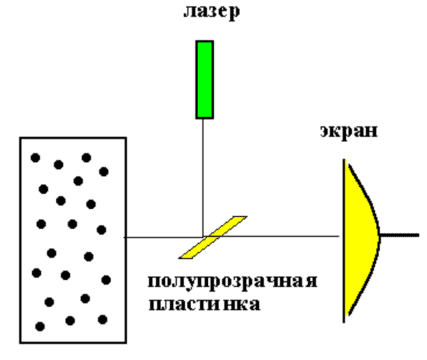
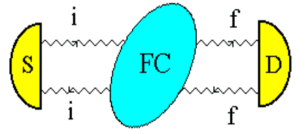
Figure 1 shows a diagram of a typical experiment on recording the PLR spectrum of the studied substances, for example, crystalline minerals.
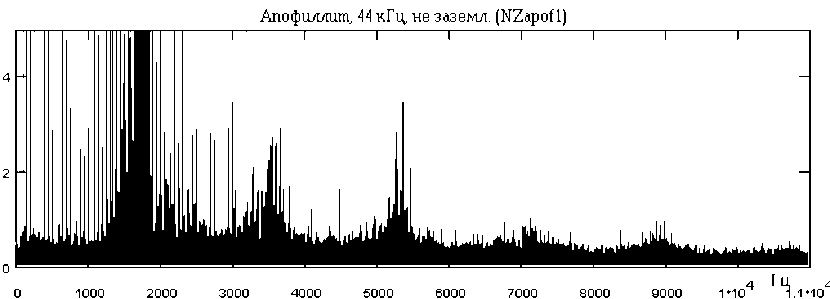
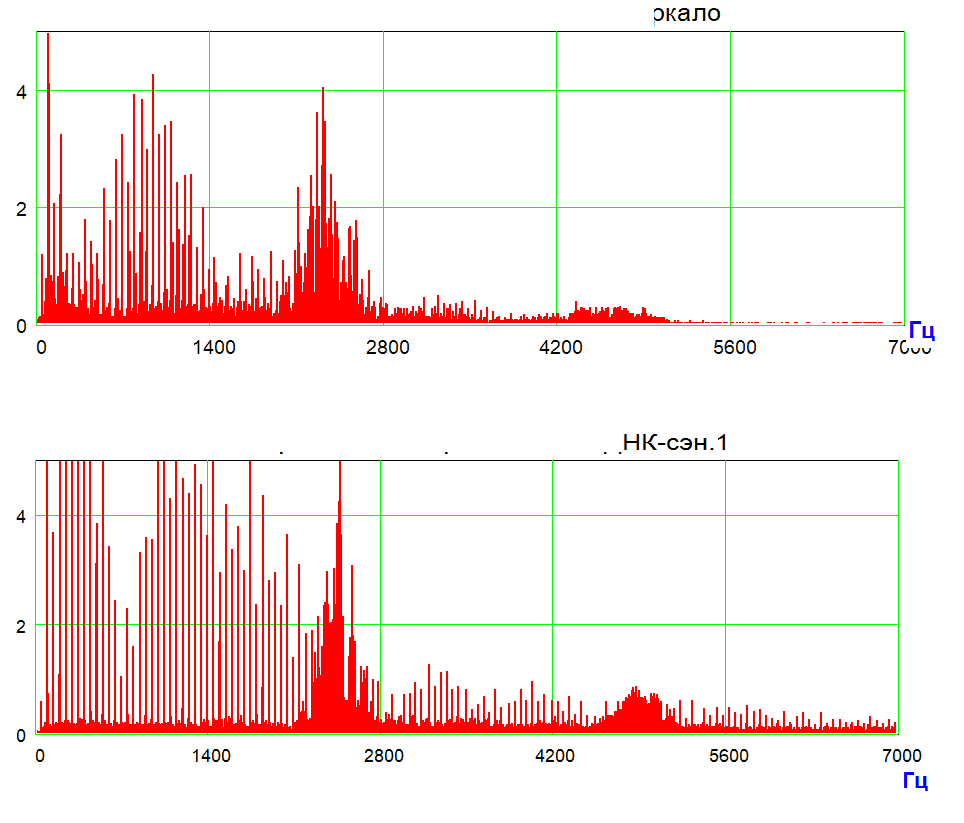
Figure 2 shows the PLR spectrum of the mineral apophyllite. The arrows indicate the region of the spectrum sweep shown in Fig. 2a.
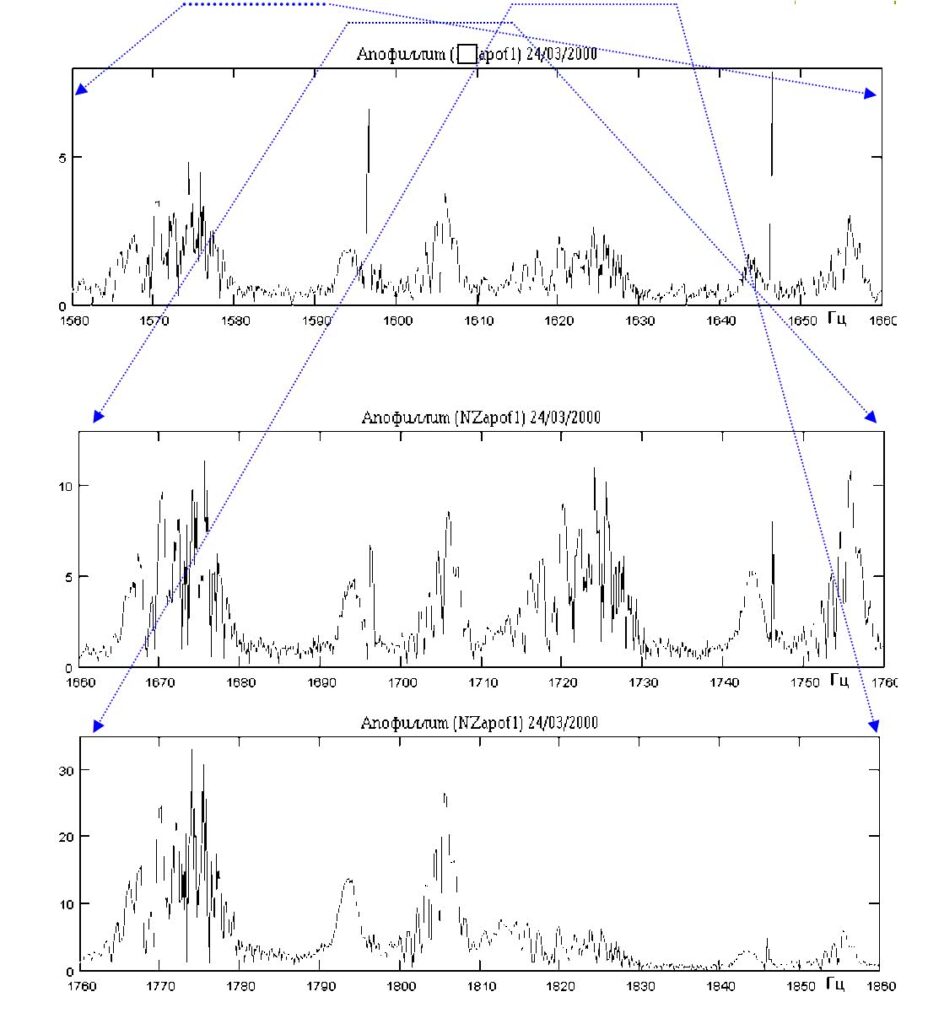
Fig.2a. Scan of the Polarization-Laser-Radiowave (PLR) spectrum of the mineral apophyllite.
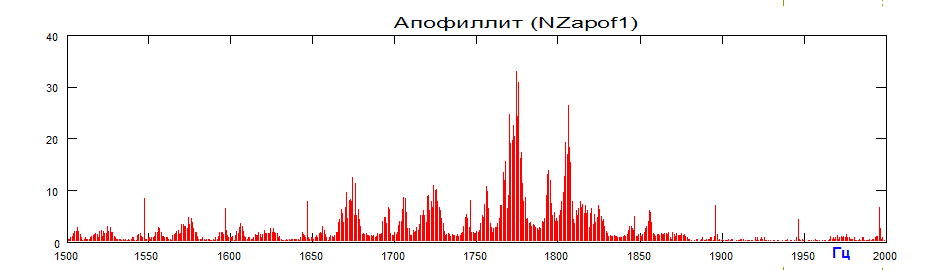
The signal sampling frequency is 44 kHz. Deployed areas 1550-1660 Hz, 1660-1760 Hz, 1760-1860 Hz. It can be seen that these regions of the spectrum have an isomorphic structure with different amplitudes. This kind of spectral modulation can be called heterofrequency modulation fractalization.
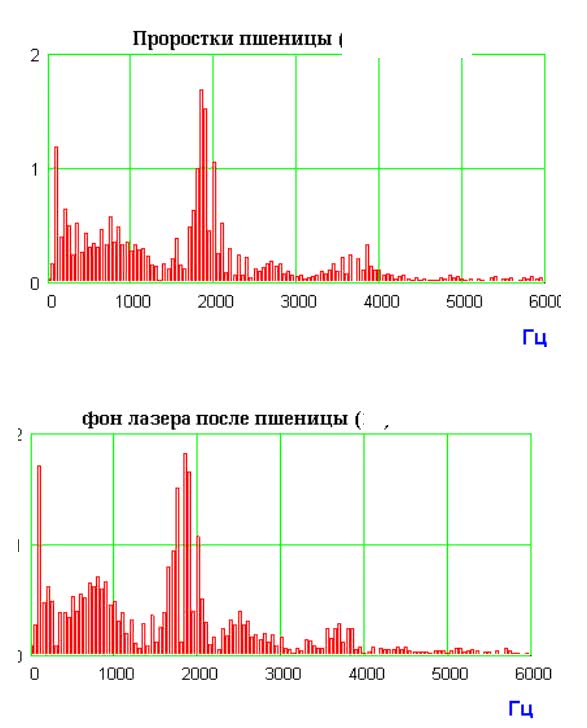
Figure 3 shows an experiment with recording the PLR spectrum (signal sampling rate – 22 kHz) of a living green leaf of a wheat seedling and spectral memory for this object. Before the experiment, as in the case with the spectra of tourmaline and apophyllite crystals, the background radio emission of the PLR spectrometer was recorded, which was typically noisy, and its amplitude decreases exponentially to 5000 Hz. For living leaves, characteristic pronounced frequency regions are found in the regions of 800-900Hz, 1700-1900Hz, 2400-2600Hz and 3600-3800Hz. After wheat seedlings are removed, the PLR spectrometer continues to generate radio emission characteristic of wheat leaves for some time. And this also manifests spectral PLR-memory.

Figure 4 shows the PLR spectra of a high-polymer DNA preparation from calf thymus (upper spectrum) and its spectral “trace” on laser mirrors (lower spectrum) after removal of the drug from the zone of the probing laser beam. As in the case of minerals and wheat leaves, one can see the closeness of the spectrum of the DNA preparation and the spectrum of its “trace”.
Biological activity of PLR spectra of DNA preparations
The DNA preparations that we used to “record” their PLR spectra through the polarization radio wave component (DNA radio waves) have a specific effect on biosystems, for which we used potato tubers, causing their abnormally fast germination (up to 1 cm/day). An experiment was also carried out three times (May 1999) on the effect of DNA radio waves on the seeds of the plant Arabidopsis thaliana (L.) Heynh affected by gamma radiation, collected in the Chernobyl nuclear power plant zone in 1986-1987.
In a typical experiment of 3 variants of exposure to seeds (1 hour 30 min, 1 hour 40 min and 2 hours; dose rate of 25 mR / hour for gamma radiation) “DNA radio waves” in the last 2, an increase in seed germination is observed compared to two controls ( P<0.001). That is, out of 300 and 200 sown seeds in the control, 2 and 4 germinated, and in the experiment, 16 and 24. However, at dose rates above 170 mR/h, the effect of “revitalization” of seeds was not observed. This suggests that radio wave radiation of DNA obtained by this method has the ability to restore the genetic apparatus and, in general, the vital activity of A. Thaliana seeds, but in limited intervals of the dose rate of gamma radiation. It is also significant that the seeds were stored for a long time (from 1987 to 1999), which led to their significant aging, which imposes an additional destructive factor. Nevertheless, a “revitalizing” effect is observed, and this suggests that DNA radio wave radiation can carry reparative genetic (metabolic) information, which confirms our early work on wave biosign repair effects on gamma-irradiated wheat and barley seeds [17 , eighteen]. It is possible that the transfer and perception of such wave information by acceptor seeds is carried out according to the mechanism of quantum nonlocality (teleportation), as we assumed earlier [5, 19], but in the modification (permissive model) proposed in this study.
Anticipating the theoretical and physical analysis of the proposed model of teleportation (see below), we will make some judgments about the significance of this problem for genetics and biology in general. The issue of quantum nonlocality of the genome has already been discussed in [5, 19]. In the present study, these ideas are formalized and therefore more substantiated. The biological experiments cited above can presumably be interpreted as a demonstration of the transfer of genetic information from DNA preparations to recipient biosystems by the mechanism of quantum teleportation in a permissive variant. It seems that the quantum nonlocality of genetic (chromosomal) information, as a manifestation of its total distribution (continuity) in the space of multicellular biosystems, is a particular case. In fact, there are at least six levels of nonlocality in biosystems.
Level 1 – organismal. Nonlocality here is expressed in the ability to regenerate, for example, in planarian worms. After cutting such worms, any part of their body gives a whole organism during regeneration. In other words, in this case there is no binding of the general pool of genetic information to any part of the biosystem. The same applies to vegetative propagation of plants.
2nd level – cellular. From each cell, and not just from the zygote, you can grow a whole organism. For animal biosystems, this is difficult, but possible. Each cell is a potential continuum of an organism.
3rd level – cellular-nuclear. Enucleation of nuclei from somatic and germ cells, followed by the introduction of other nuclei into them, does not prevent the development of a normal organism.
Cloning of this kind is already carried out in higher biosystems, for example, in sheep. Each cell nucleus is also a potential continuum of the biosystem. There is no localization of genetic potencies on any individual cells.
The 4th level is molecular: the ribosome “reads” the information RNA not only by individual codons, but by its entirety, taking into account the context, that is, non-locally, continuously.
5th level – chromosomal-holographic. The genome has a holographic memory [26], which is a typically distributed (non-local) associative memory. At this and subsequent levels, nonlocality acquires a new quality, a dualistic material-wave character, since holograms as a substance are “read” by electromagnetic and/or acoustic fields, which carry gene-wave information beyond the limits of the substance of chromosomes. The physical field or fields appear on the stage as a calibration field, marking out the future space of the organism.
Apparently, this also includes the holographic memory of the cerebral cortex, which sets the mental, semantic and figurative spaces that calibrate the potential actions of higher biosystems. In this socio-genetic processes are realized.
6th level – quantum non-locality of the genome. Up to the 6th level, the non-locality of genetic information is realized in the space of the organism. The 6th level has a special character and a new quality. It manifests itself within the framework of one of the forms of quantum nonlocality, namely the permissive one, postulated in this work. In this case, nonlocality is realized both in the space of the biosystem and in its own time, “compressible” to zero. The gene-wave programs, which are isomorphic to real ones and are instantly distributed in such ways, work in the body “here and there at the same time”, therefore the semantic construction “first and then” loses its meaning. And this is a strategic factor, an evolutionary achievement of extraordinary importance for multicellular biosystems. Billions of body cells must “know” about each other, if not all, then a lot, and instantly. Without the phenomenon of “wave information instantaneity”, a giant multicellular continuum of higher biosystems is not able to holistically coordinate metabolism, its physiological and other functions. Intercellular diffusion of signaling substances and nervous processes are too inert for this. Even if we assume that symbolic electromagnetic fields with light speeds are involved in intercellular transmission, which is quite justified, then this is not enough. The mechanism of precisely quantum nonlocality is needed, and it is applicable to the genetic apparatus, which can act as an instantly distributed quantum (wave) object isomorphic to real chromosomes [17, 18]. Using non-locality, the genetic apparatus of higher biosystems creates an amazing phenomenon when, at certain moments in the “collapsed” space-time, the biosystems “here and there”, “first and then” work as an inseparability, providing organisms with supercoherence, informational over-redundancy, over-information, connectivity and, as a result, integrity (survivability). A manifestation of this, for example, is the ability to regenerate organs and tissues in lower organisms (hydras, worms, amphibians, lizards, crustaceans), an ability that has been largely lost by man. But it can be activated, taking into account the principles of wave self-organization of biosystems that we are developing. This is illustrated by the world’s first successful engraftment of donor tissues implanted in a blind person with restoration of vision [25]. The ideology of such a surgical operation and regenerative processes was based on research [17, 18, 26].
At the same time, theoretical and experimental studies here are still of an initial nature and need physical and mathematical understanding and development. Therefore, in the next part of this work, we present a formalized model of photon-radio wave processes generated during the interaction of a laser beam with matter, processes that, in a hypothetical plan, can be considered as the basis of PLR spectroscopy and as the simplest model of wave information events in chromosomes.
Theoretical part
Localization of light in an elastic scattering channel. Ability to write and read information localized in spatially correlated heterogeneous systems
In the experimental part of this work, we presented the results indicating:
> about the possibility of reading the spectrum of intrinsic excitations of some crystals and biological structures,
> about the possibility of long-term storage of this information,
> on the possibility of subsequent reading and transmission of this information.
The experiments were carried out in the radio range using the device (PLR spectrometer) described above.
Here we offer one of the possible theoretical interpretations of these experiments. Our constructions are based on the ideas of the theory of light localization in dispersed spatially correlated systems.
The phenomenon of light localization has become widely known since 1985 after the work [1]. Now this is one of the most dynamically developing areas of physics, closely intertwined with such “fashionable” problems as, for example, quantum teleportation, new methods of recording and reading information, etc. [6,12,13].
In such cases, quantum mechanics prescribes to calculate the probability Р of a photon reversal in the following way. Each of the processes is associated with the probability amplitude a and the reversal probability (we took into account that both amplitudes under the modulus sign have the same phases – this is the peculiarity of the movement along the loop [14]). If we had a hypothetical ability to distinguish between these ways, the probability of a reversal would be considered completely different and would be half as much: . This is the formal reason for the peak in the backward direction. However, the appearance of a peak in the backward direction is by no means accompanied by a corresponding decrease in light scattering in any other direction [11]. How to be in this case with the law of conservation of energy and where did those extra photons come from that formed the peak? The second question is why this peak is not observed when light is reflected from a continuous half-space? And the third question. What makes us think that there are two ways for a photon to move between a pair of particles? If the trajectory of a photon between particles is a one-dimensional straight line, then what are two different ways to bypass it? The reversal of a photon between two scatterers is a uniquely defined procedure, shown in Fig. 6 b).
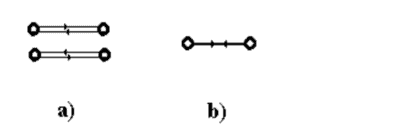
a) two ways
photon loops on it
trajectories under conditions
weak
localization.
b) photon reversal between two
particles.
So, we would very much like to have two ways for a photon to pass through an infinitely narrow loop between two particles. This can be achieved if we assume that the topological dimension of the photon trajectory under conditions of weak localization is d<1. Only in this case we can place inside one one-dimensional line of Figure 6 b) two different “lines” – a topological object similar to a loop, i.e. characterized by two ways of bypassing it.
There is an elegant mathematical construction, which, on the one hand, is very similar to what is called a line or a trajectory in physics, and, on the other hand, its topological dimension d is indeed less than one. Moreover, d=0. We are talking about the so-called. Antoine chain set [15]. This object is perfectly adapted to describe the process of continuous generation of multiscale loops on the photon trajectory.
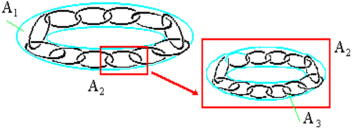
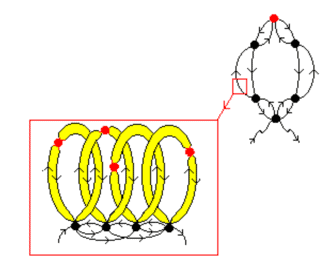
Antoine’s zero-dimensional set (Antoine’s necklace) is arranged as follows. At the first stage, a seeding “thick” closed loop А1 is considered. On the second – A1 is replaced by a chain of less “thick” links A2located inside A1. Then each link A2 is replaced by a chain of even smaller links A3 A2, and so on. Continuing this process, we get the sequence A1 A2 A3 … (see Fig. 7). The intersection of these sets is a zero-dimensional Antoine set A. The described construction is the simplest version of the Antoine set.
Despite the fact that the Antoine chain is zero-dimensional, it does not lose some of the properties of the usual one-dimensional line. So, if from the usual zero-dimensional set A0, for example, from a finite set of points, it is easy to remove the ring “threaded” through it without crossing A0 anywhere, then it is not possible to do the same with the zero-dimensional set A.
Let us assume that the photon trajectory under conditions of strong and weak localization is an Antoine set with topological dimension d=0. Interesting conclusions follow from this. If a photon moves along an Antoine trajectory, then it is rather difficult for it to leave this set. He experiences problems with access to the real world with d=1,2,3, similar to the difficulties of a person who is in a room without windows and doors. A physical interpretation of the mechanism of light confinement in the system is also possible, due to the unusual topology of the Antoine trajectories. Replacing a real three-dimensional photon by a zero-dimensional object leads to a singular nature of the energy distribution along the trajectory of the Antoine photon. Such a trajectory has a kind of “mechanical rigidity”. The intertwined “hard” links of the Antoine set resist any attempt at disengagement. This is also the reason why the photon is kept close to the pair, more precisely, close to itself.
Is it possible for an Antoine photon to enter the real world? A narrow peak in the backward direction during light scattering by a disperse system under conditions of weak localization is nothing else than the emission of Antoine photons initiated by light.
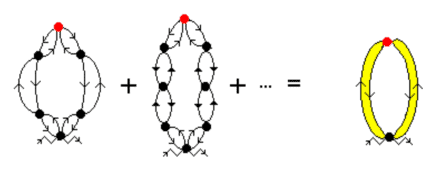
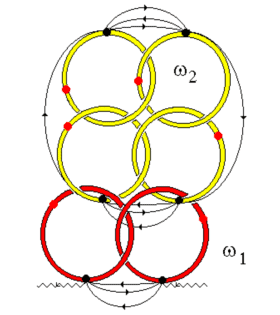
An analysis of the perturbation theory series for a photon propagator in a system of particles shows that there are trajectories isomorphic to the Antoine set. These trajectories, similar to a loop made up of two parts, like a handcuff ring, are shown in Fig. 8.
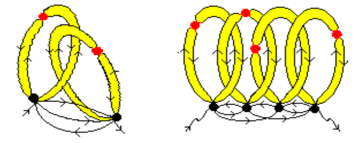
Two semirings (they are not necessarily identical) join at the top particle. The sum of such loops is indicated by us with a tinted ring. In the course of their movement, these trajectory rings can intertwine – see Fig. 9. In turn, each propagator line that makes up the intertwined rings Fig. 9, there is also a set of intertwined rings of a smaller scale (see Fig. 10) This is repeated ad infinitum.
A necessary condition for localization is a very strong renormalization or reduction in the wavelength of a photon entering the system. As is known, in systems with large values of the permittivity, the wavelength of the photon becomes much less than the wavelength of the incident photon. The frequency of the photon does not change in this case – the effective speed of the photon changes in accordance with the relation . We are interested in the situation in which , otherwise the photon will not “fit” on the vanishingly small links of the Antoine set. The effective speed of the photon then becomes zero.
One of the objects where a strong renormalization of the radiation wavelength is actually possible is a fractal cluster consisting of weakly absorbing monomer particles. Fractal systems are heterogeneous systems with scale invariance. Any small fragment of the system, when scaled up, reproduces the spatial structure of the entire system. A fractal cluster (FC) is usually called an agglomerate of micron sizes, consisting of nanometer solid particles held together by van der Waals forces. Fractal clusters are formed either as a result of highly nonequilibrium condensation of solid vapors and subsequent aggregation of nanometer-sized monomer particles, or at the initial stage of the crystallization process from solutions or melts.
The scale invariance of the cluster causes a relatively slow decrease in pair correlations in the arrangement of its particles. The pair correlation function is structured as follows
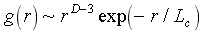
where D is the fractal dimension of the cluster, Lc – is the characteristic size of the correlation block. The fractal dimension determines the number of particles-monomers of the cluster N, located inside an imaginary sphere of radius r : N ~ rD. The value D<3 and optionally an integer – this is the specificity of a fractal cluster. In ordinary dense packings of particles, pair correlations fall off much faster, disappearing exponentially at characteristic distances of the order of several particle radii. The scale invariance of a FC is visually reflected in its rather loose structure. The density of particles in the volume r3 of a fractal cluster is not constant, but proportional to.
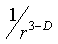
The renormalization is caused by long-range correlations in the arrangement of FC particles, which are visually expressed in the connectivity of the cluster and the presence of a large number of voids in it. This is explained as follows. Let a photon incident on the cluster with a wavelength on the order of the characteristic size of the cluster L be captured by some sufficiently large FC cavity (resonant cavity). This trapping leads to an increase in the effective permittivity of the cluster (increases near any electromagnetic resonance [16]). The increase initiates, in turn, a decrease in length
photon waves, because . A photon with a renormalized wavelength finds another cavity, smaller. A new capture again stimulates an increase and a new decrease, and so on. As a result, all cluster cavities may be filled with renormalized photons, including those with wavelength photon waves, because . A photon with a renormalized wavelength finds another cavity, smaller. A new capture again stimulates an increase and a new decrease, and so on. As a result, all cluster cavities may be filled with renormalized photons, including those with wavelength .
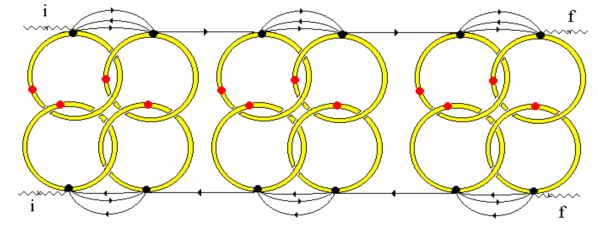
The physics of light localization in fractal systems and the calculation scheme are as follows. A photon is constantly present between the source and the radiation detector, “circulating” in a closed loop (see Fig. 11). It is held there by the intertwining of rigid Antoine rings on its trajectory (see Fig. 12). Rings are formed as a result of multiple rescattering of a photon by monomer particles of a fractal cluster. Further, the amplitude of the interaction of a pair of virtual photons is calculated, which are located inside the area designated as FC (fractal cluster) in Figure 12. One of them corresponds to the upper “shore”, the second – to the lower one. Typical processes that form this amplitude can be seen in Fig. 12 if we discard the wavy lines of real photons. The interaction amplitude is sought in the form of a solution to the corresponding Bethe-Salpeter equation. It can be shown that the imaginary part of this amplitude describes the confinement or localization of a photon in the system.
The corresponding calculation leads to the following expression for the differential cross section of elastic light scattering by a cluster [8]:

between the flux of radiation scattered in the direction nf and the flux density of the incident radiation Jnf, it can be seen that the singularity in the cross section means that a finite “current” of photons is possible in the system even at zero flux density of the incident radiation. The forward singularity describes the stimulated emission of light from the cluster. This is a typical “laser” effect. The coherence of stimulated emission is ensured by the “zero-dimensionality” of localized Antoine photons, the ability to concentrate a huge number in a small volume. The physical reason for the coherent ejection of these photons is simple and clear. Any photon scattered “sideways” is captured by the cluster and begins to oscillate in it along the scattering direction without the right to leave the cluster. Antoine rings intertwined with the corresponding rings of localized photons are formed on its trajectory. It is this entanglement that keeps such a photon in the cluster. The photon scattering at zero angle has the most such rings – the imaginary part has a maximum at (see expression (1)). And at the same time, only such a photon has the ability to escape from the cluster, which is described by the real part of the cross section. This photon, having hooked its rings on the corresponding rings of localized photons, pulls them out (see Fig. 13). So, in the language of Antoine rings, one can easily understand the physics of stimulated emission of light.
We expect that such effects, namely, the localization of light, take place in the system of correlated mirrors of the device described in [we]. Here, localization is possible between any pair of a large number of possible combinations of mirrors.
Reading and writing localized light
The spectrum of eigenexcitations of any system is largely determined by its boundary or surface. A typical example of such excitations is plasmon polaritons on a metal surface or surface plasmons in small metal particles. Is it possible to “count” the spectra characteristic of such excitations and write them down on some carrier or storage device for the purpose, for example, of long-term storage and subsequent reading? We will talk about the problems and prospects of these studies.
As is known, when a photon is reflected from a flat surface, the state of its polarization does not change – this is forbidden by the isotropy of the problem with respect to rotations in the surface plane. It would seem that even when light is reflected from a flat plate with two walls, the situation will not change. However, this is not the case if we take into account the possibility of light localization between the plate boundaries. Effects of this kind are observed when light is scattered in a strictly backward direction in a homogeneous ensemble of tiny particles [11]. This is due to the possibility of “pulling out” a photon localized in the system by a backscattered photon. In this case, the polarization of the reflected light may change. The reason why it “pulls out” a localized photon, as we know, is not related to the photon-photon interaction, which can be neglected under these conditions, but to the intertwining of the Antoine rings of the scattered and localized photons.
This effect, combined with the rotational-vibrational and polarization characteristics of the objects under study, can be used to effectively extract from the object its own excitations localized in it (its “spectrum”). Consider the circuit shown in Fig. 1. It contains the laser described above, and the crystal, whose spectrum we want to “pull” out. Another change has been made to the design of the standard laser. A translucent plate was removed from it, located at the Brewster angle to the laser axis (the purpose of this plate is to cut off parasitic light of non-primary polarization). This is done in order not to interfere with the light reflected from the crystal and changing its polarization as a result of “pulling out” localized photons from the crystal, re-enter the resonator and then repeat its route many times. We expect that the efficiency of “pulling out” localized photons that have recorded information about an object in such a system will be high enough for its experimental observation. Further, these delocalized photons can again be localized but already in the system of laser mirrors. After that, we remove the crystal, but the “spectrum” of its excitations, localized in the laser, as we expect, will manifest itself for some time. The system will reproduce the spectral memory of an object that has already been removed from the exposure area. The role of a crystal can be played by any system in which field localization is possible. For example, these can be biological objects, in particular, genetic structures that have a fractal liquid crystal packaging. It is probably this kind of spectral memory effects that was observed in our experiments (see above).
We emphasize that we are talking about the possibility of reading the entire spectrum of the object by laser radiation with a fixed frequency – in a wide frequency range. The fact is that a laser photon with a frequency “doesn’t care” which localized photon “pulls out” from an object: with the same frequency or with any other, if any.
Localized light and problems of quantum teleportation
A completely unexpected application of the idea of light localization is found in the problem of quantum teleportation – the instantaneous transmission of a message over arbitrarily long distances. This exotic area of research, starting from [2, 3], has attracted increasing attention of physicists and, more recently, biologists. Let us briefly recall the main provisions of the “classical” theory of quantum teleportation.
As is known, any wave function of a pair of photons (photon 2 and photon 3), each of which has two polarization states (horizontal polarization and vertical polarization), can be expanded in four basic states (in terms of the so-called Bell states), which form a complete orthonormal system functions [22]

The state (in what follows we will be more interested in it than the rest) has an interesting property: when one of the photons with a certain polarization is detected, the polarization of the other turns out to be opposite.
The ability to experimentally distinguish one of the Bell states from the others is provided by their different symmetries. Of the four states (2), the first three are bosonic states (their wave function does not change sign when particles 2 and 3 are interchanged). The last state is fermionic (when 2 and 3 are interchanged, the sign of the wave function changes). This feature of the state makes it possible to distinguish it in a number of experiments well described in the literature, using the interference of two specially prepared light beams [3].
Bearing in mind the possibility to work further with the state , in what follows, the following experimental scheme, which has already become classical, is used [2, 3, 22]. There are two participants in the game – Alice and Bob, and a source of a pair of photons described by the state . Alice’s task is to transfer the photon 1 she has to Bob, who is arbitrarily far away from her. However, Alice does not use the usual classical method, but proceeds as follows. Alice and Bob simultaneously receive a pair of photons 2 and 3, described by the state . Alice receives photon 2, and Bob receives photon 3. Alice “mixes” photon 1 and 2. In this case, in one case out of four, she has the opportunity to observe the state
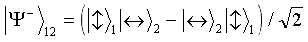
As soon as it detects this, photon 3 immediately goes into the initial state of photon 1. The reason for this is as follows. Alice’s observation of a state means that at some state of photon 1, photon 2 will be in the opposite polarization state. But since photons 2 and 3 are also in the state , photon 3 will be in a state orthogonal to state 2, i.e. in the state of photon 1. Thus, photon 1 is teleported from Alice to Bob, regardless of the distance between them. Teleportation is instantaneous.
True, with such teleportation, the polarization state of the teleported photon 1 is unknown to Alice, since photon 1 mixes with photon 2, forming a state.
The described teleportation procedure is flawless from the point of view of the formalism of quantum mechanics. Nevertheless, the physical meaning of Bell’s basic states remains unclear, just as there is no complete clarity in the resolution of the Einstein-Podolsky-Rosen paradox (EPR paradox) [4], for the description of which these states, in fact, were introduced. How to understand that when measuring the polarization of one of the photons, which are, for example, in the state, the polarization of the other instantly turns out to be, despite the fact that they are separated by a very large distance and any information regarding the state of the second can come to us after a very certain period of time.
Pairs of photons described by states (2) or their linear combinations are usually called EPR photons or entangled photons. Until we understand the physical reason for the instantaneous correlations in the properties of these photons, we will not understand the physics of teleportation, despite the flawlessness of the logical constructions.
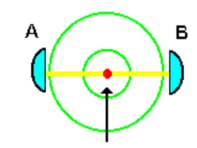
Surprising as it may seem, the problems of the EPR paradox and teleportation can also be approached from the other side, from the point of view of the existence of localized light. One of the variants of the EPR paradox is the following. Consider, for example, s-scattering of a photon by a spherical particle, i.e. the scattered wave is spherically isotropic (see Fig. 14). Let the scattered photon approach the detector at point A (Alice). This act of registration allows us to conclude that at theDoes teleportation contradict the foundations of the special theory of relativity, which states that the speed of information transfer cannot exceed the speed of light? Obviously not. In the case of Bennett-type teleportation [2, 3], an unknown signal is instantly transmitted to no one. In our model, nothing is transmitted at all. Bob gets what is already next to him, but for the time being, is inaccessible to him. The information already exists. Alice instantly “allows” Bob to take her. Therefore, we called such a modification of quantum teleportation (nonlocality) permissive (from the English “permission” – permission). It should also be noted that such nonlocality apparently extends further, since in our case the photons modulated by the object are instantly (nonlocally) converted into radio waves that store “photon polarization information”. It is also possible that in our experiments probing the object and interfering counter photons record a dynamic polarization hologram of the object, such as DNA, and turn it into a bioactive radio wave isomorphic photon hologram. same moment in time this scattered photon reaches the detector, located, for example, at point B (Bob), arbitrarily far from A. This is despite the fact that any information from B to A can be transmitted after only a well-defined period of time. If we do not consider the possibility of superluminal speed of signal propagation, the situation can be understood as follows. What if the registered act of arrival of light in A is connected not at all with a scattered photon, but with a localized “long” photon knocked down from the “tube” AB? We “catch” its left “end”. Then in the fact that at the same moment of time there is a “registration” at point B of its “right” the end, there is nothing strange. There is no superluminal signal propagation, just as there is no signal propagation at all. The “long” localized photon is pulled out of the “cavity” due to the meshing of the rigid Antoine rings of the localized and scattering photons. This link is similar to the link in a fractal cluster considered above.
Let us now assume that there is no photon scattered by the particle. And there is a “cavity” between Alice and Bob, filled with a photon localized in it. Alice sends her photon into this cavity. This photon hooks a localized photon according to the mechanism known to us and provides it to Bob. Thus, as a result of Alice’s actions, Bob immediately receives some information, though it is not known what, since many properties of a localized photon are unknown to anyone.
As we can see, in this case, for instantaneous “transmission” of a signal, instead of a pair of EPR-correlated photons, it is enough to deal with a single localized photon (however, if desired, it can be considered as a pair of virtual photons interacting with each other – an upper-bank photon and a lower-bank photon). banks of figures 1 and 2). In addition, in [3], the EPR pair teleported an unknown photon of Alice to Bob. In our case, Alice’s photon, acting on the left end of an unknown localized photon, provides its right end to Bob. This is the whole difference and similarity of the two teleportation mechanisms.
Does teleportation contradict the foundations of the special theory of relativity, which states that the speed of information transfer cannot exceed the speed of light? Obviously not. In the case of Bennett-type teleportation [2, 3], an unknown signal is instantly transmitted to no one. In our model, nothing is transmitted at all. Bob gets what is already next to him, but for the time being, is inaccessible to him. The information already exists. Alice instantly “allows” Bob to take her. Therefore, we called such a modification of quantum teleportation (nonlocality) permissive (from the English “permission” – permission). It should also be noted that such nonlocality apparently extends further, since in our case the photons modulated by the object are instantly (nonlocally) converted into radio waves that store “photon polarization information”. It is also possible that in our experiments probing the object and interfering counter photons record a dynamic polarization hologram of the object, such as DNA, and turn it into a bioactive radio wave isomorphic photon hologram.
sources:
- Albada P. van, Lagendijk A., Observation of Weak Localization of Light in a Random Medium, Phys. Rev. Lett. 55, 1985, p. 2692-2695.
- Bennet C.H., Brassard G., Crepeau C., Jossa R., Peres A., Wootters W.K., Teleporting and unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett., v. 70, p. 1895-1899 (1993).
- Bouwmeester D., Pan Jian-Wei, Mattle K., Eibl M., Weinfurter H., Zeilinger A., Experimental quantum teleportation. Nature, v. 390, p. 575-579 (1997).
- Einstein A., Podolsky B., Rosen N., Can quantum-mechanical description of physical reality be considered complete? // Phys.Rev. 1935, v.47, p.777-780.
- Gariaev P., Tertishny G. The quantum nonlocality of genomes as a main factor of the
- Lagendijk A., van Tiggelen B.A., Resonant Multiple Scattering of Light, Physics Reports, v. 270, p. 143-216, 1996.
7.Lushnikov A.A., Maksimenko V.V., Simonov A.J., Electromagnetic Surface Modes in Small Metallic Particles, in Electromagnetic Surface Modes, ed. by A.D. Boardman, J. Wiley, Chichester, 1982, pp. 305-345. - Maksimenko V.V., Antoine’s Localization of Photon inside Fractal Cluster, Fractal in Engineering, Delft, Netherlands, 1999, p. 355-358.
9.Maksimenko V.V., Localization of Light in Fractal Cluster, J. of Aerosol Science, v. 30, 1999, p. 287-288.
10.Maksimenko V.V., Localization of Photon between Pair of Particles-2. Inelastic Scattering, J. of Aerosol Science, v. 30, 1999, p. 289-290.
morphogenesis of biosystems. // 3th Scientific and medical network continental members meeting. Potsdam, Germany. May 6-9, 1999, p.37-39. - Maximenko B.V.,. Krikunov V.A. Lushnikov A.A., Strong localization of light in close-packed granular media, JETP, vol. 102, 1992, p.1571.
- Sheng P. (Ed.), Scattering and Localization of Classical Waves in Random Media. World Scientific. Signapore, 1990.
- Sheng P., Introduction to Wave Scattering, Localization, and Mesoscopic Phenomena. Academic, San Diego, 1995.
- Abrikosov A.A., Fundamentals of the theory of metals. The science. Moscow, 1987, p.183.
- Boltyansky V. G., Efremovich V. A. Visual topology, Moscow, Nauka, 1982, p. 84.
- Boren K., Huffman D., Absorption and scattering of light by small particles. Moscow, Mir, 1986, p. 77.
- Garyaev P.P. Wave genetic code. M. 1997. Publishing Center. 108s.
- Garyaev P.P. wave genome. M. Public benefit. 1994. 279p.
- Garyaev P.P., Garber M.R., Leonova E.A., Tertyshny G.G. On the question of the central dogma of molecular biology. Consciousness and physical reality. 1999, Ed. FOLIUM. V.4, No. 1, pp. 34-46.
- Garyaev P.P., Tertyshny G.G. The phenomenon of the transition of light into radio waves in relation to biosystems. Collection of scientific papers. Academy of Medical and Technical Sciences of the Russian Federation. Department of “Biotechnical systems and education” at MSTU. N.E. Bauman. 1997, Issue 2. p. 31-42.
- Garyaev P.P., Tertyshny G.G., Gotovsky Yu.V. Transformation of light into radio waves. III International Conference “Theoretical and Clinical Aspects of Application of Adaptive Resonance and Multiresonance Therapy”. “IMEDIS”. Moscow. April 18-20, 1997 pp. 303-313.
- B. B. Kadomtsev, Dynamics and Information, Moscow, Editorial Board of the journal “Uspekhi fizicheskikh nauk”, 1999, 400 pp.
- L. D. Landau and E. M. Lifshitz, Quantum Mechanics, Moscow, Nauka, 1974, 752 p.
- Lushnikov A.A., Maksimenko V.V., Quantum optics of a metal particle, ZhETF, vol. 103, 1993, pp. 1010-1044.
- Muldashev E.R. Combined eye transplantation. Ministry of Health of the Russian Federation, All-Russian Center for Eye and Plastic Surgery. “Alloplant”, 2000.
- Prangishvili I.V., Garyaev P.P., Tertyshny G.G., Leonova E.A., Mologin A.V., Garber M.R., Genetic structures as a source and receiver of holographic information, Sensors and Systems , No. 2, 2000, p.2-8.
- Cheng R. and Furtak T. (eds) Giant Raman scattering. Moscow. Mir, 1984, 408 p.